최단경로
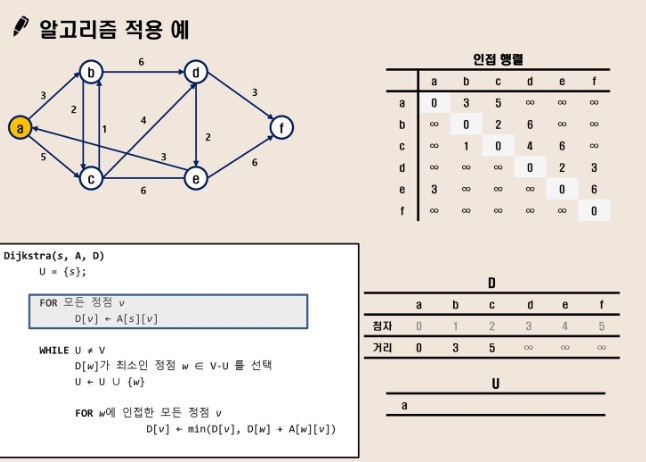
Dijkstra 알고리즘
“하나의 정점에서 다른 모든 정점까지의 최단 경로를 구하는 문제”에 대하여 다익스트라 알고리즘을 사용한다.
- 간선들은 모두 양의 간선들을 가져야 한다.
문제 : 아래 그래프에서 0부터 다른 모든 정점까지의 최단거리
6 11
0 1 3
0 2 5
1 2 2
1 3 6
2 1 1
2 4 6
2 3 4
3 4 2
3 5 3
4 0 3
4 5 6
답 : [0, 3, 5, 9, 11, 12]
 ※ 그림은 진행과정이다
※ 그림은 진행과정이다
소스코드
- 첫 정점을 기준으로 연결되어있는 정점들을 추가해가며, 최단 거리를 갱신한다.
- 정점이 연결되기 전까지는 시작점을 제외한 정점들은 모두 무한대 값을 가진다.
- 시작점은 첫정점이므로 0이다.
- A-B-C가 있다면 A에서 C까지의 최단거리는 ‘A와 B의 최단거리 + B와 C의 최단거리’가 된다.
import java.util.Arrays;
import java.util.Scanner;
public class Dijkstra {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int V = sc.nextInt();
int E = sc.nextInt();
int[][] adj = new int[V][V];
for (int i = 0; i < E; i++) {
// 유향그래프
adj[sc.nextInt()][sc.nextInt()] = sc.nextInt();
}
// 각 정점까지의 최단거리가 저장될 배열
int[] dist = new int[V];
// 방문체크배열
boolean[] visited = new boolean[V];
// 첫번째 노드를 방문하고, 첫번째 노드로부터 경로가 있는 간선은 경로비용을 dist에 써주고 없는 곳은 무한대를 적어주자.
// 시작점을 0으로 잡고, 0에서 0의 거리는 어차피 0이므로 1부터 시작
visited[0] = true;
for (int i = 1; i < V; i++) {
dist[i] = adj[0][i];
if (adj[0][i] == 0)
dist[i] = 987654321;
}
// 출발정점은 최단거리가 0으로 이미 됐으니 하나 빼고 V-1개에 대해서 최단거리를 찾자.
for (int i = 0; i < V - 1; i++) {
int min = 0; // 제일 가까운 친구의 정점번호를 저장할 변수
int minVal = 987654321;
for (int j = 0; j < V; j++) {
// 아직 방문 안했으면서, dist가 제일 작은 값을 찾자.
if (!visited[j] && minVal > dist[j]) {
min = j;
minVal = dist[j];
}
}
// dist중에 젤 작았던 min으로부터 출발해서 갈 수 있는 경로비용과 기존에 알고있던 경로비용 중 작은값으로 dist업데이트
// 그러니까, 첫 시작 노드랑 연결이 안되었지만,다른 정점을 거쳐서 갈 수 있는 최단경로를 찾는다.
// min은 거쳐서 갈수있는 다른 정점인것이고, minVal은 시작노드에서 min까지의 최단경로이다.
// dist[j] > dist[min] + adj[min][j] : 시작노드에서 바로 가는것과, 거쳐서 가는 것중 최소인 것을 찾는 것
for (int j = 0; j < V; j++) {
if (adj[min][j] != 0 && dist[j] > dist[min] + adj[min][j]) {
dist[j] = dist[min] + adj[min][j];
}
}
visited[min] = true;
}
System.out.println(Arrays.toString(dist));
}
}
