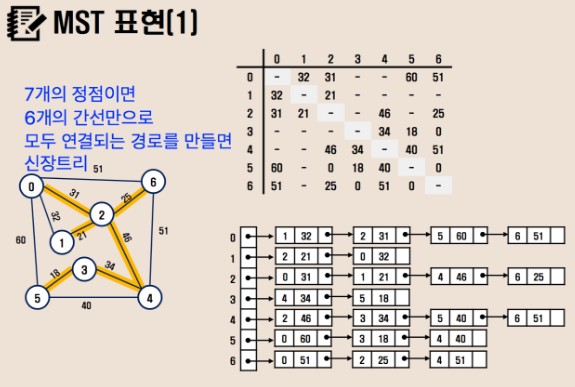
Spanning Tree (신장 트리, 스패닝트리)

그래프 내의 모든 정점을 포함하는 트리. 그래프의 최소 연결 부분 그래프이다.

간선의 수가 가장 적은 최소 연결 그래프
n개의 정점을 가지는 그래프의 최소 간선의 수는 (n-1)개
하나의 그래프에는 많은 신장트리가 존재할 수 있다
모든 정점들이 연결되어 있어야 하고 **사이클을 포함해서는 안된다.**

MST(Minimum Spanning Tree, 최소 신장 트리)

Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리

간선의 가중치의 합이 최소
n개의 정점을 가지는 그래프에 대해 (n-1)개의 간선만을 사용
사이클이 포함되지 않아야 함

그래프에서 최소 비용 문제

1) 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리 (Kruskal MST-간선중심) 2) 두 정점 사이의 최소 비용의 경로 찾기(Prim MST-정점중심)

문제 : 아래 그래프의 최소신장트리의 최소비용

답 : 175

MST

Kruskal MST

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;

public class Kruskal {
	static int[] parents;
	static int[] rank;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int V = sc.nextInt(); // 정점의 갯수 : 7
		int E = sc.nextInt(); // 간선의 갯수 : 11
		int[][] edges = new int[E][3]; // 출발정점, 도착정점, 비용

		for (int i = 0; i < E; i++) { // 무향그래프
			edges[i][0] = sc.nextInt();
			edges[i][1] = sc.nextInt();
			edges[i][2] = sc.nextInt();
		}

		// edge배열을 비용순으로 오름차순 정렬한다.
		Arrays.sort(edges, new Comparator<int[]>() { //  선택정렬, 오름차순
			@Override
			public int compare(int[] o1, int[] o2) {
				return Integer.compare(o1[2], o2[2]);
			}
		});
		// V개의 정점만큼 상호배타집합을 위한 parents배열을 생성한다(rank는 옵션)
		parents = new int[V];
		rank = new int[V];

		// V개의 정점들을 모두 makeSet해서 각자 독립된 집합으로 만들어 준다.
		for (int i = 0; i < V; i++) {
			makeSet(i);
		}
		// edge배열을 탐색하면서 가장 짧은 간선의 출발-도착 정점이 서로 다른 집합일면 간선을 선택하고 두 집합을 합친다.
		// V-1개의 간선이 선택되면 종료
		int sum = 0;
		for (int i = 0; i < E; i++) {
			int a = edges[i][0];
			int b = edges[i][1];
			int c = edges[i][2];

			// 출발점 정점 findSet, 도착점 정점 findSet
			// 둘이 다르다면 경로비용 누적합하고 union
			if (findSet(a) != findSet(b)) {
				sum += c;
				union(a, b);
			}
		}
		System.out.println(sum);
	}

	static void makeSet(int x) {
		parents[x] = x;
		rank[x] = 0;
	}

	// 최상위에 부모가 누군지 찾기
	static int findSet(int x) {
		if (parents[x] == x)
			return x;
		parents[x] = findSet(parents[x]);
		return parents[x];
	}

	static void union(int x, int y) {
		int px = findSet(x);
		int py = findSet(y);

		if (rank[px] > rank[py])
			parents[py] = px;
		else {
			parents[px] = py;

			if (rank[px] == rank[py])
				rank[py]++;
		}
	}
}

Prim MST (간선이 많을수록 prim을 사용하는것이 좋다)

1) ArrayList

import java.util.ArrayList;
import java.util.Scanner;

public class Prim_ArrayList {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int V = sc.nextInt();
		int E = sc.nextInt();

		int[][] adj = new int[V][V];
		for (int i = 0; i < E; i++) { // 인접행렬
			int a = sc.nextInt();
			int b = sc.nextInt();
			int c = sc.nextInt();
			adj[a][b] = c;
			adj[b][a] = c;
		}

		// ArrayList를 하나 준비해서 이곳에 방문해서 내편이 된 정점을 담음.
		ArrayList<Integer> list = new ArrayList<>();
		boolean[] visited = new boolean[V];
		// 첫번째 0번 노드를 방문함 -> 0을 ArrayList에 담고, 방문체크
		list.add(0);
		visited[0] = true;

		// V-1개의 정점을 선택할때까지. V-1번 반복
		// list안 의 모든 정점을 출발지로 하는 간선중에 가장 작은 간선의 도착정점을 방문체크하고 list에 추가
		int sum = 0;
		for (int i = 0; i < V - 1; i++) {
			int min = 987654321;
			int minIdx = 0;

			for (int start : list) {
				for (int j = 0; j < V; j++) {
					if (adj[start][j] != 0 && min > adj[start][j] && !visited[j]) {
						min = adj[start][j];
						minIdx = j;
					}
				}
			}
			list.add(minIdx);
			sum += min;
			visited[minIdx] = true;
		}
		
		System.out.println(sum);
	}
}

2) Priority Queue

import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.Scanner;

public class Prim_Priority_Queue {
	static class Node implements Comparable<Node> {
		int dest;
		int cost;

		Node(int d, int c) {
			dest = d;
			cost = c;
		}

		@Override
		public int compareTo(Node o) {
			// TODO Auto-generated method stub
			return Integer.compare(this.cost, o.cost);
		}
	}

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int V = sc.nextInt();
		int E = sc.nextInt();

		ArrayList<Node>[] adj = new ArrayList[V];
		for (int i = 0; i < V; i++) {
			adj[i] = new ArrayList<>();
		}
		for (int i = 0; i < E; i++) { // like 인접행렬
			int a = sc.nextInt();
			int b = sc.nextInt();
			int c = sc.nextInt();

			adj[a].add(new Node(b, c));
			adj[b].add(new Node(a, c));
		}

		boolean[] visited = new boolean[V];
		PriorityQueue<Node> queue = new PriorityQueue<>();

		visited[0] = true;
		queue.addAll(adj[0]); // adj[0]의 데이터가 전부 add 됨
		int cnt = 0;
		int sum = 0;

		while (!queue.isEmpty()) {
			if (cnt == V)
				break;
			Node node = queue.poll();
			if (visited[node.dest])
				continue;

			// 방문한적이 없으면 가중치를 누적합하고 해당 정점을 방문체크, 그리고 그 정점으로 출발하는 모든 간선 큐에 삽입
			sum += node.cost;
			queue.addAll(adj[node.dest]);
			visited[node.dest] = true;
			cnt++;
		}
		
		System.out.println(sum);

	}
}